Inductor est communis componentia passiva ad energiam servandam in circuitis, fungens functionibus sicut filtratio, boost, et buck in designo potentie commutativae. In initio designi schematis, ingenii non solum oportet eligere convenientes valores inductivitatis, sed etiam considerare correntem quam inductor sustinere potest, DCR spire, dimensiones mechanicae, amissos, et cetera. Si non sunt satis familiari cum functionibus inductoris, saepe erunt passivi in designo et consument multum temporis.
Intelligendo Functiones Inductorium
Inductor est littera "L" in circuito filtro LC ad exitum potentie commutativae. In conversione buck, unum terminum inductoris conectit ad voltam DC exitus, dum alter terminus commutat inter voltam input et GND secundum frequentiam commutationis.
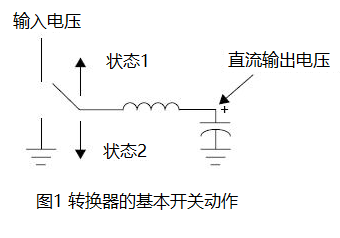
In statu 1, inductor conectitur ad voltam input per MOSFET. In statu 2, inductor conectitur ad GND.
Propter usum huius generis controller, sunt duae methodi ut terram coniungas inductorem: terra per diodum aut per MOSFET. Si prior methodus adhibetur, converter vocatur modo asynchrone. In altero casu, converter dicitur esse in modo synchrone.
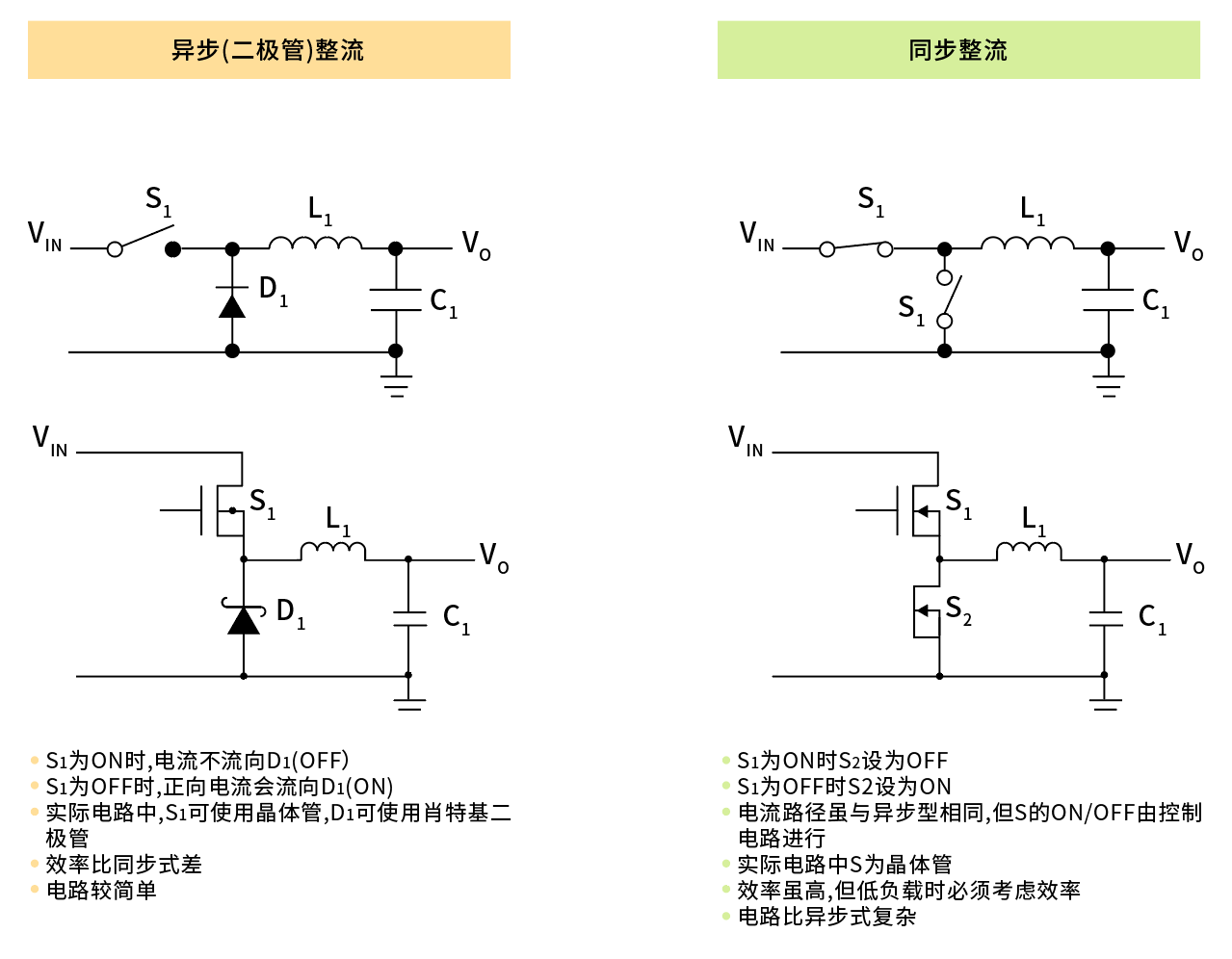
In statu 1, unum caput inductoris coniungitur ad voltatem input, et alterum caput coniungitur ad voltatem output. Propter converter buck, voltas input necesse est esse maiorem quam voltas output, ita fit drop voltatis forward super inductore.
In statu 2, caput inductoris prius coniunctum ad voltam input nunc coniungitur ad terrain. Propter converter buck, voltas output necessario est terminus positivus, ita fit drop voltatis negativus super inductore.
Formula Calculationis Voltatis Inductor
V=L(dI/dt). Cum cursus per inductorem crescens sit cum voltus inductorii positivus est (Status 1) et decrescit cum voltus negativus est (Status 2), forma undarum cursus inductorii monstratur in Figura 2:
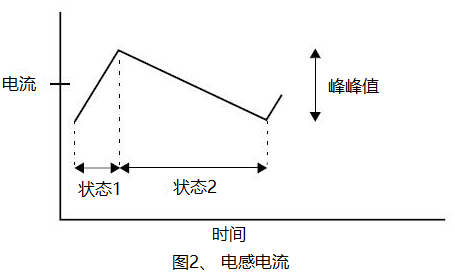
Ex figura praecedente, videmus quod maximum cursus per inductorem est cursus DC addito dimidio amplitudinis cursus commutationis. Praedicta figura item indicat cursus fluctuationem. Secundum formulam praedictam, cursus maximus computari potest hoc modo: ubi ton tempus est in Statu 1, T periodus commutationis est, et DC cyclus officii Status 1 est.
Circuitus Conversionis Synchronus
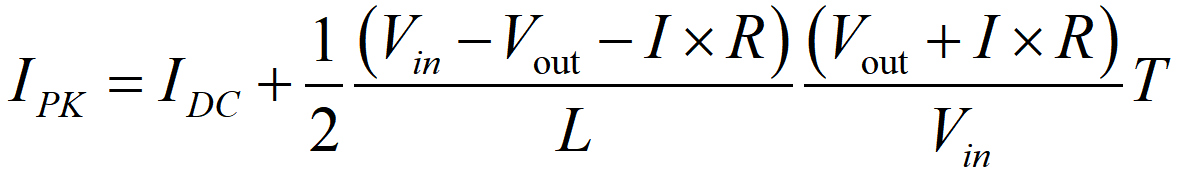
Circuitus Conversionis Asynchronus
Rs: Resistentia coniuncta resistoris sensibilis et resistentiae involucrum inductorium. Vf: Depressio voltus ante Schottky diodum. R: Totalis resistentia in via conductiva, calculata ut R=Rs+Rm, ubi est resistentia status inclusi MOSFET.
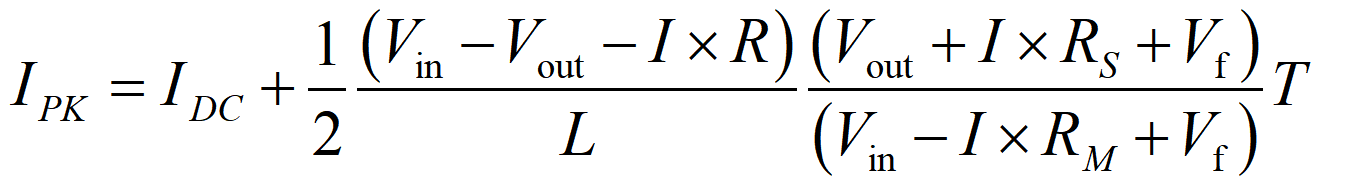
Saturatio Nuclei Inductor
Ex calculato summitati currente inductor, scimus quod cum crescens est cursus per inductorem, eius inductio marcescet. Hoc definitur per physicas proprietates materiae nucleo. Gradus inductionis marcentis est crucialis: si marcentia nimis severa est, converter non operabitur normaliter. Cursus quo inductor deficiet propter nimium currentem vocatur saturatio currentis, parametri fundamentalis inductor.
Curva saturationis inductorum potentiae in circuitibus converter est crucialis et digna attentione. Pro intelligendo huius conceptus, potes observare actualiter mensuram curvam L versus DC currentem.
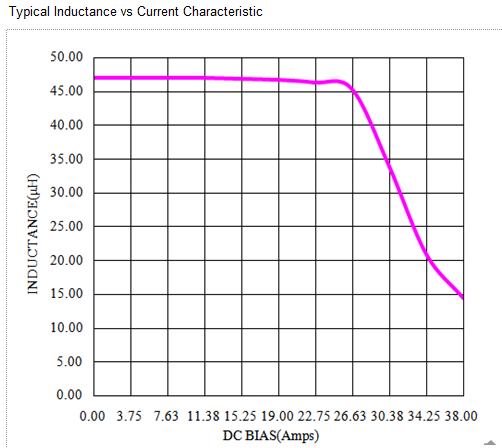
Cum crescit ultra certum limen, inductio repente decrescit—phenomenon quod saturatio dicitur. Plus incrementa currentis possunt causare ut inductor penitus deficiat.
Hoc characteristico saturationis, intellegere possumus cur omnes converteres specificent variationem rangi inductivitatis (△L ≤ 20% aut 30%) sub directo currente output, et cur specificatio inductoris includat parametrum Isat. Cum mutatio in corrente undulationis non significanter affectet inductivitatem, desideratur in omnibus applicationibus minimizare quam maxime correntem undulationis, quia haec affectat undulationem voltaminis output. Hinc semper magna sollicitudo est de gradu attenuationis inductivitatis sub directo currente output, dum inductivitas sub corrente undulationis saepe neglecta est in specificitationibus.
Selectio Inductorum Appropriorum pro Alimentationibus Electricis Commutativis
Inductores sunt componentes communiter utilitati in alimentariis commutatoribus. Propter differentiam phasium inter suam praesentem et voltam, theoricam, amissio nulla est. Inductores saepe funguntur ut elementa storationis energiae, habentes proprietatem "resistendo introeunti et conservando exeuntem," et saepe coniunguntur cum capacitoribus in circuitibus filtrorum input et output ad praebendam praesentiam lenem.
Ut componentes magnetici, inductores intrinsecus obviam fiunt problema magneticæ saturatiónis. Quædam applicationes patiuntur saturatiónem inductoris, aliæ permittunt saturatiónem ex certa valore currus incipiendi, dum aliæ eam severé prohibent, differentiam in circuitibus specificis postulantes. In plurimis casibus, inductores in regione "lineari" operantur, ubi valor inductivitatis constans manet et non variatur cum voltage terminale vel cursu. Tamen, fontes vim mutatorum non negabilem probléma habent: inductore volutæ introducunt duos distributos (vel parasiticós) parametrós. Unus est resistencia volutæ inevitabilis, alter autem capacitatem dispersam ad processum volutæ et materiales referens. Capacitas dispersa minimum impactum habet ad bassas frequentiás, sed eius effectus magis manifestus fit cum frequentia crescit. Cum frequentia certum valorem superat, inductor potest proprietates capacivæ exhibere. Si capacitatem disperse "aggregatam" ut unicum capacitoris consideramus, circulus æquivalens inductoris suam naturam capacivam ultra certam frequentiam revelat.
Cum statum operationis inductoris in circuito analyzandum est, sequentia characteristica consideranda sunt:
1. Cum cursus I per inductorem L fluat, energia in inductore conservata est: E=0.5 × L× I2(1)
2. In cyclo commutandi, relatio inter variationem cursus inductoris (valorem pici-pici undarum) et voltam inter inductorem est:
V=(L × di)/dt(2), Quod ostendit magnitudinem undarum esse coniunctam valoribus inductivitatis.
3. Inductores item processus impletionis et exsolutionis peragunt. Cursus per inductorem est proportionalis integrali voltaminis (volt-sectundorum) super eum. Dummodo voltamen inductoris mutetur, etiam ratio mutationis cursus di/dt mutabitur: voltamen antecedens facit ut cursus lineariter ascendet, dum contra voltamen facit ut descendet.
Selectio Inductorium pro Alimentariis Electricis Commutatis Buck-Typus
Quando indactorium eligis pro alimentario electrico commutato buck-typus, necesse est ut maximam voltam inputalem, voltam outputalem, frequentiam commutationis potentiae, maximam cruentam fluctuationis, et circulum officii determines. Subsequens descriptio computi valoris inductivitatis pro alimentario electrico commutato buck-typus continet. Primum, praesumamus quod frequentia commutationis sit 300 kHz, ambitus voltae inputalis sit 12 V ± 10%, cruentas outputalis sit 1 A, et cruenta maxima fluctuationis sit 300 mA.
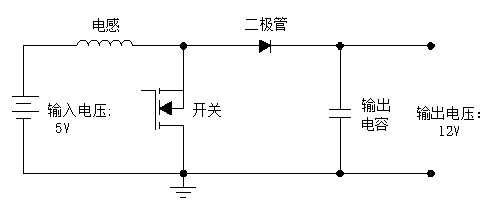
Diagramma Circuitarum Alimentarii Electrici Commutati Buck-Typus
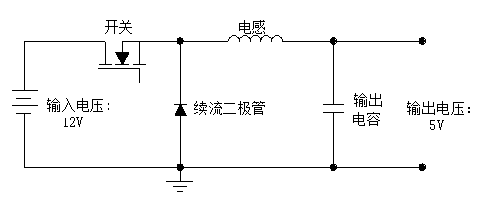
Tensionis input maximae voltatilis est 13.2V, et responsiva proportio officii est: D=Vo/Vi=5/13.2=0.379(3), ubi Vo est tensio output et Vi est tensio input. Cum transitor commutandi est inpositus, voltas inductoris est: V = Vi - Vo = 8.2 V(4). Cum transitor commutandi est demissus, voltas inductoris est: V=-Vo-Vd=-5.3V(5).dt=D/F(6). Substituentes aequationes (2), (3), et (6) in aequationem (2):
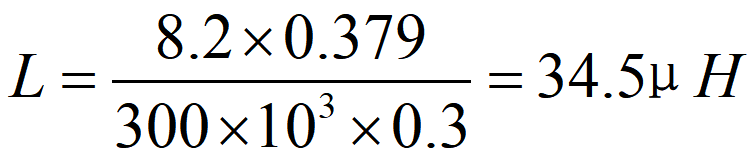
Selectio Inductorium pro Commutandis Alimentariis Typi Boost
Calculatio valoris inductivitatis pro alimentatore potentiae commutativae boost, praeterquam quod formula relationis inter cyclum officii et voltam inductoris mutatur, ceteri processus sunt eiusdem modi ac metodi calculi alimentatoris potentiae commutativae buck. Praesupponendo quod frequentia commutationis sit 300 kHz, ambitus tensionis input sit 5 V ± 10%, cursus output sit 500 mA, et efficientia sit 80%, maximus cursus fluctuationis sit 450 mA, et correspondens cylcus officii sit: D = 1 - Vi/Vo = 1 - 5.5/12 = 0.542 (7).
Diagramma circuitus alimentatoris potentiae commutativae boost
Cum interruptor est conexus, voltas trans inductorem est: V = Vi = 5.5 V (8), Cum interruptor est discexus, voltas trans inductorem est: V = Vo + Vd - Vi = 6.8 V (9), Substituentes formulas 6/7/8 in formulam 2 dat:
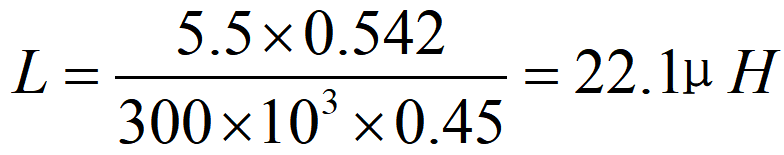
Notandum est quod, contra convertidores buck, convertidores boost non continenter praebent currentem ad onus ex inductore. Cum transitor commutatoris conductet, currentum inductoris fluat per transitorem ad terrain, dum currentum oneris praebetur ab capacitatore exitii. Proinde, capacitator exitii debet conserere sufficientem energiam ad praebendum onus durante hoc tempore. Tamen, cum commutator sit off, currentum inductoris non solum praebet onus sed etiam implet capacitator exitii.
Communiter, augens valorem inductivitatis minuit fluctuationem exitii sed deterioret responsionem dynamicam praebendi potentiae. Propterea, optima inductivitas eligenda est secundum requisita applicationis specificae. Frequenciae commutationis maiiores permitunt valores inductivitatis minores, minuentes magnitudinem inductoris et servantes spatium PCB. Ita, praebitiones potentiae commutativae modernae tendunt ad frequencias maiores ad satisfaciendum demandam pro productis electronicis minoribus.
Analytica et Applicatio Suppliorum Potentiae Commutatorii
De Lege Lenz: In circuitu per potentiam DC motum, propter suam inductam spiralis, vis electromotiva (EMF) inducitur quae resistentiam contra incrementum curriculi praebet. Itaque, in momento accensionis, cursus circuitus fere nihil est, et tota depressio voltatium fit super spira. Currens deinde paulatim crescit dum depressio voltatium super spiram minuitur ad nihilum, significans finem status transitorii. In operatione commutatoris, inductor non debet saturari ut efficientem storationem et transfusionem energie conservet. Inductor saturatus similis est viae directae per DC, amittens potestatem suam storative, quod converteris operationem subvertit. Quando frequentia commutationis fixa est, valor inductivus satis magnus esse debet ut saturationem praeveniat sub maximis curriculis.
Determinatio Inductionis in Alimentariis Commutatis: Ad inferiores frequentias commutationis, cum durationes 'on/off' sint longiores, maior valor inductionis necessarius est ad conservandum exitum continuatum. Hoc permittit inductori magis energiam campi magnetici conservare. Praeterea, periodi commutationis longiores resultabunt in renovatione energetica minus frequente, quod ad currentem fluctuationem relativam minorem ducit. Hoc principium per formulam explicari potest: L = (dt/di) * uL ubi D = Vo/Vi (cyclo operativus), dt = D/F (tempus 'on'), F = frequentia commutationis, et di = fluctuatio currus. Pro converteribus 'buck', D = 1 - Vi/Vo; pro converteribus 'boost', D = Vo/Vi. Reordinando fit: L = D * uL / (F * di). Cum F decrescit, L proportionabiliter crescere debet. Converse, crescenti L ceteris paribus, di (fluctuatio currus) minuitur. Ad frequentias superiores, crescens inductio impedimentum auget, quod ad amissam potentiam maiorem et efficientiam minorem ducit. Generaliter, cum frequentia fixa sit, maior L reductionem fluctuationis exitus promovet sed responsionem dynamicam deterioret (lentior adaptatio ad variationes oneris). Proinde, inductio optima secundum requisita applicationis eligenda est ut reductionem fluctuationis et performance transitoria equilibrio conciliet.

