En spole är ett vanligt energilagringskomponent i kretsar, och spelar roller som filtrering, höjning och sänkning i designen av växlingsströmförnäringar. I den tidiga fasen av schemadesignen behöver ingenjörer inte bara välja lämpliga induktansvärden, utan också överväga strömmen som spolen kan stå emot, DCR:n för spolen, mekaniska dimensioner, förluster och så vidare. Om de inte är tillräckligt bekanta med funktionerna hos spolar kommer de ofta att vara passiva i designen och förbruka mycket tid.
Förståelse av spolers funktioner
En spole är 'L' i LC-filtreringskretsen vid utgången av en växlingsströmförnäring. I buck-konvertering är ena änden av spolen ansluten till DC-utgångsspanningen, medan den andra änden växlar mellan inmatningsspänningen och GND enligt växlingsfrekvensen.
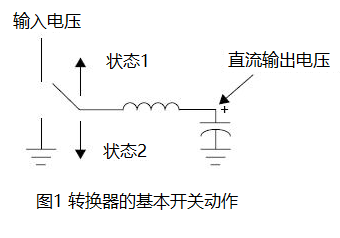
I tillstånd 1 är spolen ansluten till inmatningsspänningen via MOSFET. I tillstånd 2 är spolen ansluten till GND.
På grund av användningen av detta typ av reglare finns det två sätt att jorda spolelementet: jordning via en diod eller via en MOSFET. Om den första metoden används kallas omvandlaren för asynkron läge. I det senare fallet kallas omvandlaren för synkront läge.
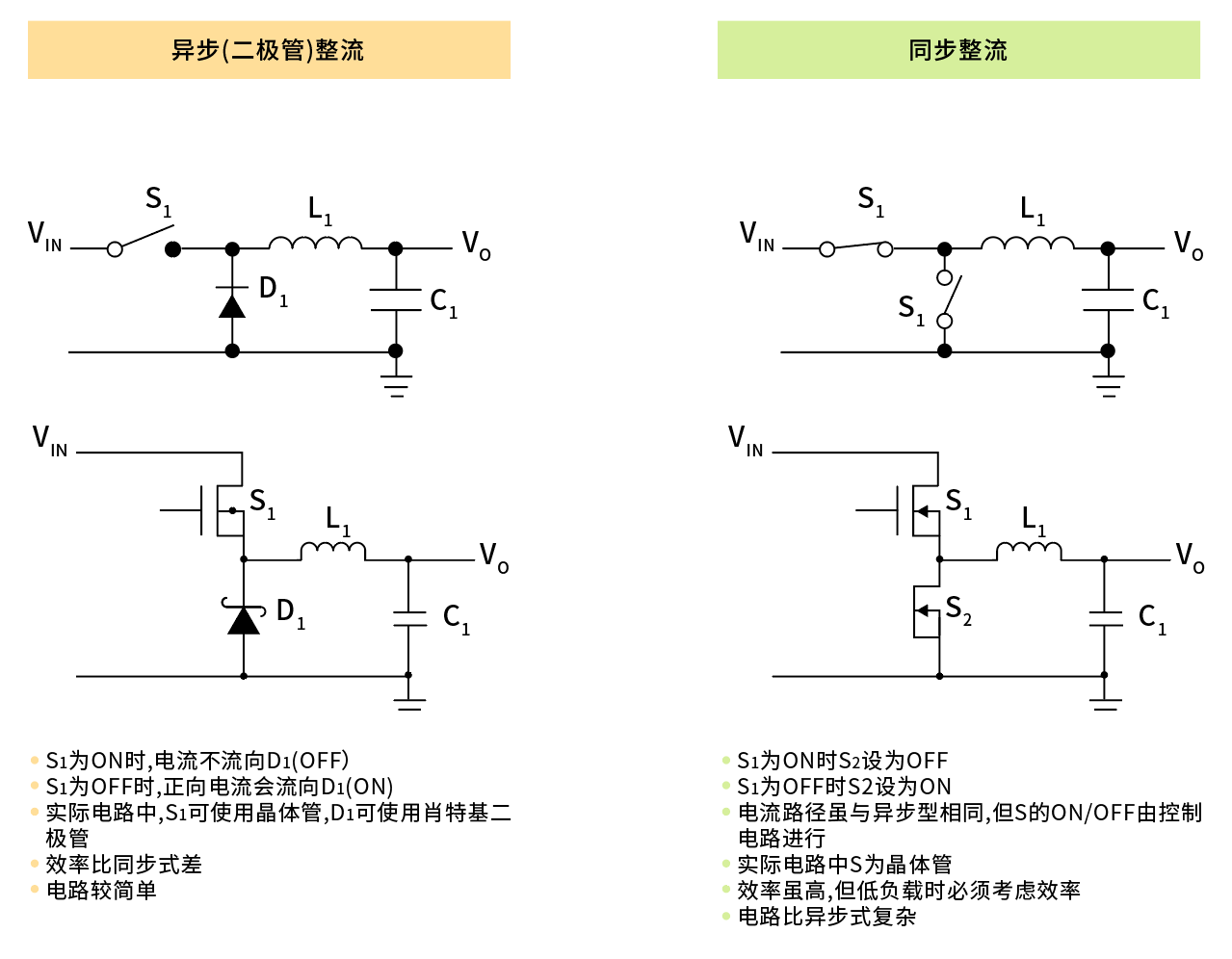
I tillstånd 1 är ena änden av spolelementet ansluten till indata-spenningen, och den andra änden är ansluten till utdata-spenningen. För en buck-omvandlare måste indata-spenningen vara högre än utdata-spenningen, så ett framåt riktat spänningsfall bildas över spolelementet.
I tillstånd 2 ansluts den änden av spolelementet som tidigare var ansluten till indata-spenningen till jord. För en buck-omvandlare är utdata-spenningen nödvändigtvis den positiva terminalen, så ett negativt spänningsfall bildas över spolelementet.
Formel för beräkning av spolelementets spänning
V=L(dI/dt). Eftersom strömmen genom spolelementet ökar när spänningsläget är positivt (Tillstånd 1) och minskar när spänningen är negativ (Tillstånd 2), visas spolelementets strömkurva i figur 2:
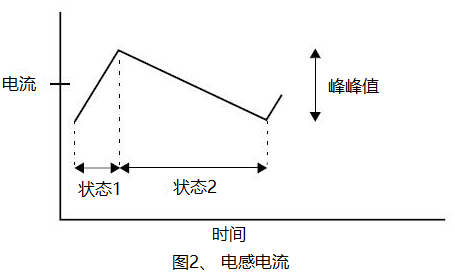
Från figuren ovan kan vi se att den maximala strömmen genom spolelementet är likströmsströmmen plus hälften av byteströmsspetsvärdet. Figuren ovan visar också rippströmmen. Enligt formeln som nämns ovan kan spetsströmmen beräknas på följande sätt: där ton är tiden i tillstånd 1, T är bytestiden och DC är driftcykeln för tillstånd 1.
Synkron omvandlingskrets
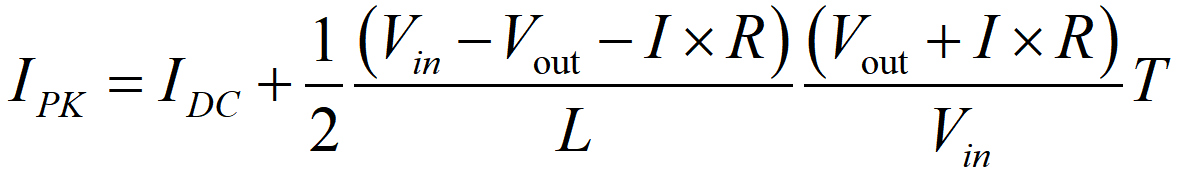
Asynkron omvandlingskrets
Rs: Den kombinerade resistansen av strömsensorns resistor och spolans viktwiktsresistans. Vf: Framställningsspänningsfall för Schottky-dioden. R: Totala resistansen i ledningsvägen, beräknad som R=Rs+Rm, där är MOSFETs påståndsresistans.
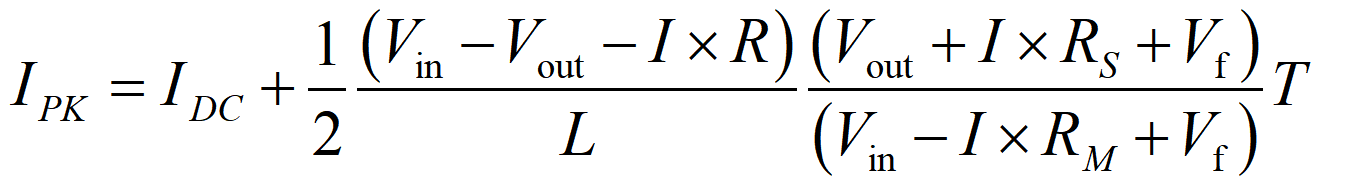
Sättning av kärnan i spolelementet
Från den beräknade spetsströmmen i spolelementet vet vi att när strömmen genom spolen ökar kommer dess induktans att minska. Detta bestäms av de fysiska egenskaperna hos kärnmaterial. Graden av induktansminskning är avgörande: om minskningen är för stark kommer omvandlaren inte att fungera normalt. Strömmen vid vilken spolen misslyckas på grund av överdriven ström kallas för sättningsström, en grundläggande parameter för spolen.
Sättningskurvan för effektspolar i omvandlarcirklar är viktig och värd att notera. För att förstå detta koncept kan du observera den faktiskt mätta kurvan för L vs. DC-ström.
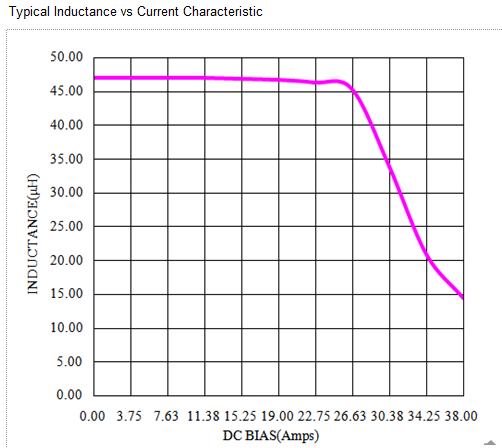
När strömmen ökar över ett visst tröskelvärde sjunker induktansen skarpt – ett fenomen som kallas sättning. Ytterligare ökningar av strömmen kan orsaka att spolen helt slutar fungera.
Med denna mättningskaraktär kan vi förstå varför alla konverterare anger variationen i induktansvärdet (△L ≤ 20% eller 30%) under DC-utgångscströmmen, och varför spolens specifikation inkluderar parametern Isat. Eftersom förändringen i rimpelström inte påverkar induktansen på ett betydande sätt, är det önskvärt i alla tillämpningar att minimera rimpelströmmen så mycket som möjligt, eftersom den påverkar utgångsspanningens rimpel. Därför finns det alltid stor oro för graden av induktansbortfall under DC-utgångscströmmen, medan induktansen under rimpelströmmen ofta överges i specifikationerna.
Välj av passande spolar för switchande strömförsörjningar
Induktörer är vanligt förekommande komponenter i spänningsreglare med spårningskrets. På grund av fasdifferensen mellan strömmen och spänningen, är förlusten teoretiskt sett noll. Induktörer fungerar ofta som energilagradelement, med karaktäristiken att "motverka det inkommande och behålla det utgående", och används ofta tillsammans med kondensatorer i ingångs- och utgångsfiltrerande kretsar för att jämnställa strömmen.
Som magnetiska komponenter står spolar naturligtvis inför problemet med magnetisk sättning. Vissa tillämpningar tillåter sättning av spolarna, andra tillåter sättning från en viss strömnivå, medan andra strikt förbjuder det och kräver skillnad i specifika kretsar. I de flesta fall fungerar spolar i den "linjära regionen", där induktansvärdet förblir konstant och inte ändras med terminalspänning eller ström. Dock har switchande strömförsörjer ett icke försumbart problem: spolavvikningen introducerar två distribuerade (eller parasitära) parametrar. Den ena är den oundvikliga avvikningsmotståndet och den andra är den distribuerade straykapaciteten som är relaterad till avvikningsprocessen och materialerna. Straykapaciteten har minimal inverkan vid låga frekvenser, men dess effekt blir alltmer uppenbar när frekvensen stiger. När frekvensen överstiger en viss nivå kan spolen visa kapacitiva egenskaper. Om straykapaciteten "samlas" som en enskild kondensator, avslöjar den ekvivalenta kretsen för spolen dess kapacitiva beteende över en viss frekvens.
När man analyserar driftstatusen för en spole i en krets måste följande egenskaper beaktas:
1. När en ström I flöder genom en spole L, är den energi som lagras i spolen: E=0,5 × L× I2(1)
2. I ett schyttring cykel, är relationen mellan spolen strömvariation (rippelströms topp-till-topp värde) och spolans spänning:
V=(L × di)/dt(2), Detta visar att rippelströmens storlek är relaterad till induktansvärdet.
3. Spolar går också igenom laddnings- och avladdningsprocesser. Strömmen genom en spole är proportionell mot integralen av spänningen (volt-sekunder) över den. Så länge spolans spänning ändras, kommer även strömändringshastigheten di/dt att ändras: en framåtbrytande spänning orsakar att strömmen stiger linjärt, medan en bakåtbrytande spänning orsakar att den sjunker linjärt.
Utval av spolar för buck-typade switchande strömförsörjningar
Vid val av en spole för en buck-typad switchande strömförsörjning måste man avgöra den maximala inmatningspåspanningen, utgångsspänningen, effektswitchningsfrekvensen, maximala riktningsströmmen och driftschemat. Följande beskriver beräkningen av spolvärdet för en buck-typad switchande strömförsörjning. Först antar vi att switchningsfrekvensen är 300 kHz, inmatningspåspanningsområdet är 12 V ± 10%, utgångsströmmen är 1 A och den maximala riktningsströmmen är 300 mA.
Cirkeldiagram för buck-typad switchande strömförsörjning
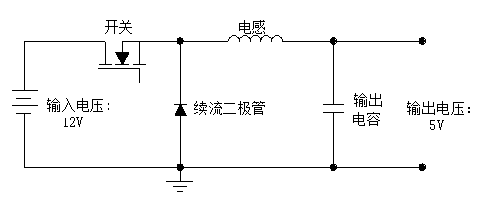
Maximal inmatningsspänning är 13,2V, och den motsvarande dutycykeln är: D=Vo/Vi=5/13,2=0,379(3), där Vo är utgångsspänningen och Vi är ingångsspänningen. När växlingstransistorn är på, är spänningsfallet över kondensatorn: V = Vi - Vo = 8,2 V(4). När växlingstransistorn är av, är spänningsfallet över kondensatorn: V=-Vo-Vd=-5,3V(5). dt=D/F(6). Genom att substituera ekvationer (2), (3) och (6) i ekvation (2):
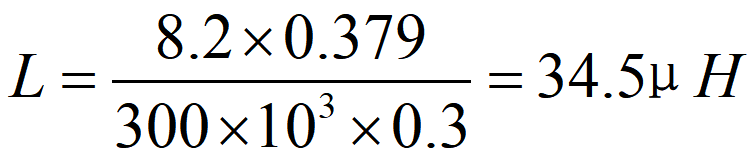
Utval av spolar för step-up-växlingsströmförsörjningar
Beräkningen av induktansvärdet för en boost-switchande strömförsörjning, utom att relationsformeln mellan driftsikten och spolespanningen ändras, är de andra processerna samma som beräkningsmetoden för en buck-switchande strömförsörjning. Antag att växelfrekvensen är 300 kHz, indataspänningsintervallet är 5 V ± 10%, utströmmen är 500 mA, och effektiviteten är 80%, den maximala rippströmmen är 450 mA, och motsvarande driftsikt är: D=1-Vi/Vo=1-5.5/12=0.542(7).
Schematiskt diagram över en boost-switchande strömförsörjning
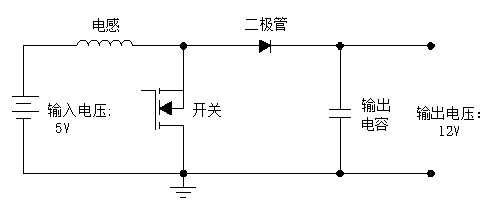
När switchen är på, är spänningen över spolen: V = Vi = 5.5 V (8), När switchen är av, är spänningen över spolen: V = Vo + Vd - Vi = 6.8 V (9), Genom att substituera formler 6/7/8 i formel 2 får man:
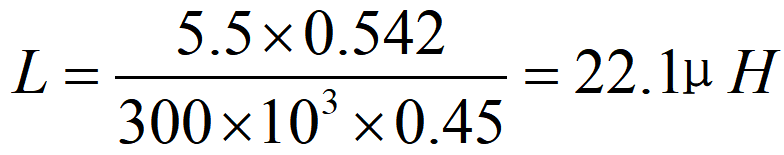
Observera att, motsats till buck-konverterare, boost-konverterare inte kontinuerligt levererar lastström från spolen. När växeltransistorerna är ledande flödar spolströmmen genom växeln till jord, medan lastströmmen ges av utgångskondensatorn. Därför måste utgångskondensatorn lagra tillräckligt med energi för att försörja lasten under denna period. Men när växeln är av, så levererar spolströmmen inte bara lasten utan laddar också upp utgångskondensatorn.
Generellt sett minskar en ökad induktansvärde utslagsripporna men försämrr dynamisk respons hos strömförsörjningen. Därför bör den optimala induktansen väljas baserat på specifika tillämpningskrav. Högre växelfrekvenser möjliggör mindre induktansvärden, vilket minskar storleken på spolen och sparar plats på PCB:n. Som ett resultat går moderna växelströmförsörjningar allt mer mot högre frekvenser för att uppfylla efterfrågan på mindre elektroniska produkter.
Analys och tillämpning av spänningsomvandlare med växlingskraft
Angående Lenz lag: I en DC-driven krets, på grund av spolens självinduktion, induceras en elektromotiv kraft (EMK) som motverkar ökningen av strömmen. Därför är strömmen i kretsen effektivt noll vid tändningen, och hela spänningsfallet inträffar över spolen. Strömmen ökar sedan alltmer när spolens spänning minskar till noll, vilket markerar slutet på den övergångstillståndet. I drift av växlingskonverterare får spolen inte gå in i mättnad för att säkerställa effektiv energilagring och -överföring. En mättad spole beter sig som en direkt DC-anslutning, och förlorar sin förmåga att lagra energi, vilket underminerar konverterarens funktionalitet. När växlingsfrekvensen är fix, måste induktansvärdet vara tillräckligt stort för att förhindra mättnad under högspetsströmmar.
Bestämning av induktans i spänningsomvandlare: Vid lägre spänningsväxlingsfrekvenser, eftersom på/av-tiderna är längre, krävs en större induktansvärde för att bibehålla kontinuerlig utgång. Detta gör det möjligt för spolelementet att lagra mer magnetisk fältenergi. Dessutom resulterar längre växlingsperioder i mindre ofta uppfyllande av energin, vilket leder till relativt mindre strömrapp. Denna princip kan förklaras genom formeln: L = (dt/di) * uL där D = Vo/Vi (driftscykel), dt = D/F (på-tid), F = växlingsfrekvens, och di = strömrapp. För buck-konverterare, D = 1 - Vi/Vo; för boost-konverterare, D = Vo/Vi. Om vi omorganiserar ger detta: L = D * uL / (F * di). När F minskar måste L öka proportionellt. I motsatsen, att öka L medan andra parametrar hålls konstanta minskar di (strömrapp). Vid högre frekvenser, ökar induktansen impedansen, vilket leder till ökad effektförlust och reducerad effektivitet. Generellt sett, med fixerad frekvens, större L minskar utgångsrapp men försämras dynamisk respons (sakta anpassning till laständringar). Därför bör den optimala induktansen väljas baserat på tillämpningskraven för att balansera mellan rappsminskning och transientsvar.

